# some_RE 题目

# ez_z3

一道来自 NSSCTF 举办的逆向专题比赛 round#x 的题目

(NSSCTF 和 NKCTF 时间重复了两边都在看题 = =)

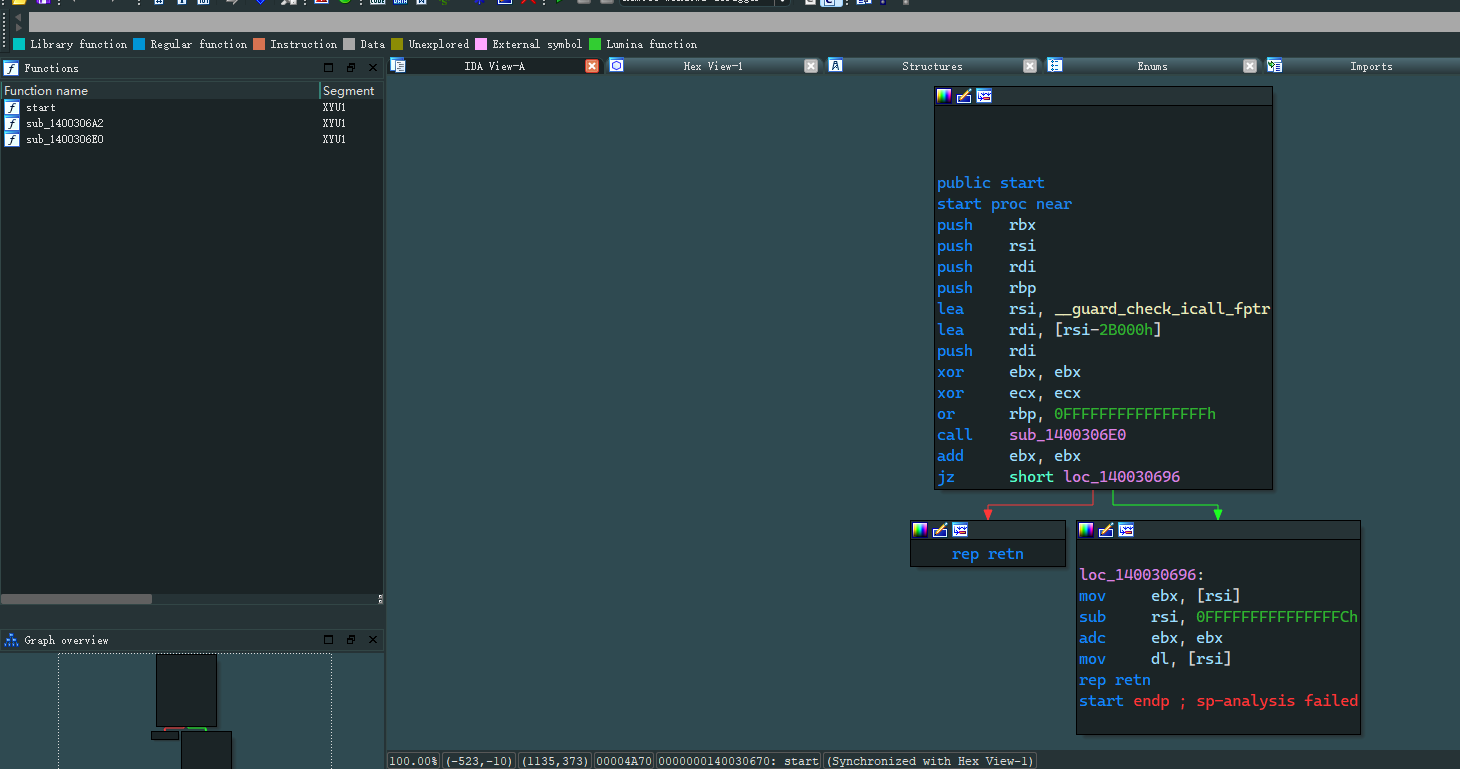
在 IDA 中看很明显看到加了壳直接脱 UPX 不行魔改了 010 中查看发现就是改了字节头的加壳直接在 010 中搜索 XYU1 改成 UPX! 就行了

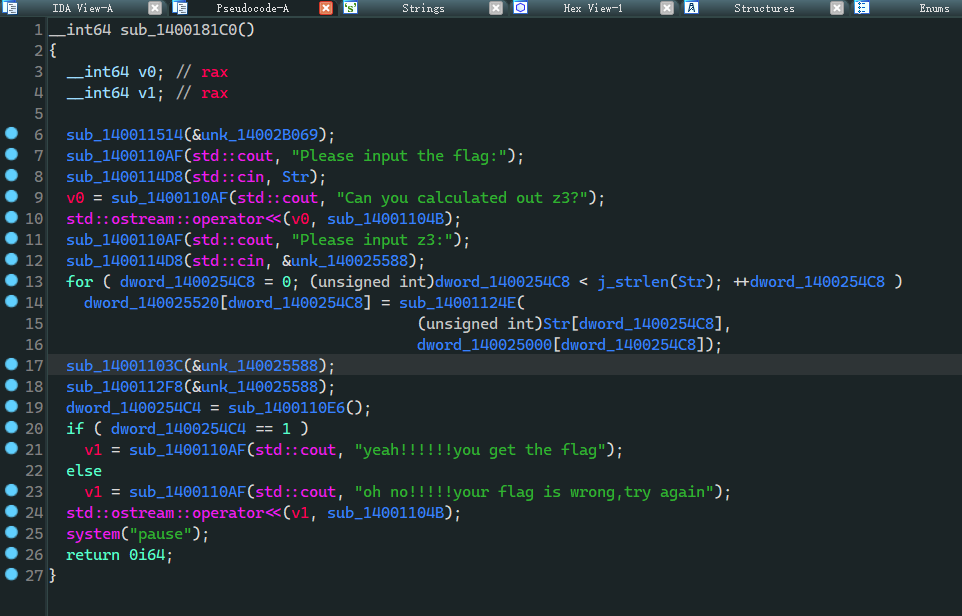
成功脱壳后在 IDA 中看到主程序 2 次输入其中在第二个输入后越过循环看到一个需要 z3 解的函数

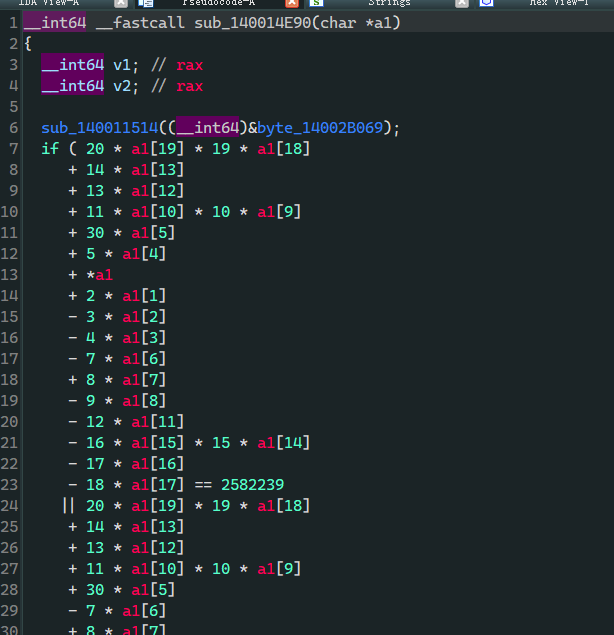
直接解就行了

上脚本

	from z3 import *
	a1 = [BitVec('x%d' % i, 32) for i in range(20)]
	s = Solver()
	for i in range(20):
	s.add(a1[i] < 127) # 添加约束条件①因为输入的肯定是可见字符
	s.add(a1[i] >= 32)
	s.add(
	20 * a1[19] * 19 * a1[18]
	+ 14 * a1[13]
	+ 13 * a1[12]
	+ 11 * a1[10] * 10 * a1[9]
	+ 30 * a1[5]
	+ 5 * a1[4]
	+ a1[0]
	+ 2 * a1[1]
	- 3 * a1[2]
	- 4 * a1[3]
	- 7 * a1[6]
	+ 8 * a1[7]
	- 9 * a1[8]
	- 12 * a1[11]
	- 16 * a1[15] * 15 * a1[14]
	- 17 * a1[16]
	- 18 * a1[17] == 2582239)
	s.add(
	20 * a1[19] * 19 * a1[18]
	+ 14 * a1[13]
	+ 13 * a1[12]
	+ 11 * a1[10] * 10 * a1[9]
	+ 30 * a1[5]
	- 7 * a1[6]
	+ 8 * a1[7]
	- 9 * a1[8]
	+ 5 * a1[4]
	+ 3 * a1[2]
	+ 2 * a1[1] * a1[0]
	- 4 * a1[3]
	- 12 * a1[11]
	- 16 * a1[15] * 15 * a1[14]
	- (18 * a1[17]
	+ 17 * a1[16]) == 2602741)
	s.add(19 * a1[18]
	+ 18 * a1[17]
	+ 14 * a1[13] * 13 * a1[12]
	+ 12 * a1[11] * 11 * a1[10]
	+ 9 * a1[8]
	+ 7 * a1[6] * 30 * a1[5]
	+ a1[0]
	- 2 * a1[1]
	- 4 * a1[3] * 3 * a1[2]
	- 5 * a1[4]
	+ 8 * a1[7]
	- 10 * a1[9]
	- 15 * a1[14]
	- 17 * a1[16] * 16 * a1[15]
	- 20 * a1[19] == 2668123)
	s.add(20 * a1[19] * 19 * a1[18]
	+ 14 * a1[13]
	+ (13 * a1[12] + 11 * a1[10] - 12 * a1[11]) * 10 * a1[9]
	+ 30 * a1[5]
	+ 5 * a1[4]
	+ a1[0]
	+ 2 * a1[1]
	- 3 * a1[2]
	- 4 * a1[3]
	- 7 * a1[6]
	+ 8 * a1[7]
	- 9 * a1[8]
	- 16 * a1[15] * 15 * a1[14]
	- 17 * a1[16]
	- 18 * a1[17] == 2520193)
	s.add(
	18 * a1[17]
	+ 17 * a1[16]
	+ 15 * a1[14]
	+ 13 * a1[12] * 12 * a1[11]
	+ 10 * a1[9]
	+ 9 * a1[8] * 8 * a1[7]
	+ 3 * a1[2] * 2 * a1[1] * a1[0]
	- 4 * a1[3]
	- 5 * a1[4]
	- 30 * a1[5]
	- 7 * a1[6]
	- 11 * a1[10]
	- 14 * a1[13]
	- 16 * a1[15]
	- 19 * a1[18]
	- 20 * a1[19] == 8904587)
	s.add(
	18 * a1[17]
	+ 7 * a1[6] * 30 * a1[5] * 5 * a1[4]
	+ 4 * a1[3]
	+ 8 * a1[7]
	+ a1[0]
	- 2 * a1[1]
	- 3 * a1[2]
	- 9 * a1[8]
	- 11 * a1[10] * 10 * a1[9]
	- 16 * a1[15] * (13 * a1[12] + 12 * a1[11] - 14 * a1[13] - 15 * a1[14])
	- 17 * a1[16]
	- 19 * a1[18]
	- 20 * a1[19] == 1227620874)
	s.add(20 * a1[19] * 19 * a1[18]
	+ 17 * a1[16]
	+ 14 * a1[13]
	+ 13 * a1[12]
	+ 12 * a1[11] * 11 * a1[10] * 10 * a1[9]
	+ 7 * a1[6] * 30 * a1[5]
	+ 5 * a1[4]
	+ 3 * a1[2]
	+ a1[0]
	+ 2 * a1[1]
	+ 4 * a1[3]
	+ 8 * a1[7]
	- 9 * a1[8]
	- 16 * a1[15] * 15 * a1[14]
	- 18 * a1[17] == 1836606059)
	s.add(
	20 * a1[19] * 19 * a1[18]
	+ 16 * a1[15] * 15 * a1[14]
	+ 14 * a1[13]
	+ 13 * a1[12]
	+ 12 * a1[11]
	+ 7 * a1[6] * 30 * a1[5]
	+ 5 * a1[4]
	+ 2 * a1[1] * a1[0]
	- 3 * a1[2]
	+ 4 * a1[3]
	+ 8 * a1[7]
	- 9 * a1[8]
	- 10 * a1[9]
	- 11 * a1[10]
	- 17 * a1[16]
	- 18 * a1[17] == 8720560)
	s.add(20 * a1[19] * 19 * a1[18]
	+ 14 * a1[13]
	+ 13 * a1[12]
	+ 11 * a1[10] * (10 * a1[9] + 30 * a1[5] + 5 * a1[4] + 4 * a1[3] - 7 * a1[6] + 8 * a1[7] - 9 * a1[8])
	+ a1[0]
	+ 2 * a1[1]
	- 3 * a1[2]
	- 12 * a1[11]
	- (16 * a1[15] - 17 * a1[16] - 18 * a1[17]) * 15 * a1[14] == 11387045)
	s.add(
	20 * a1[19] * 19 * a1[18]
	+ 16 * a1[15] * 15 * a1[14]
	+ 14 * a1[13]
	+ 11 * a1[10] * 10 * a1[9]
	+ 9 * a1[8]
	+ 3 * a1[2]
	+ a1[0]
	- 2 * a1[1]
	+ 4 * a1[3]
	- 5 * a1[4]
	- 30 * a1[5]
	- 7 * a1[6]
	+ 8 * a1[7]
	- 12 * a1[11]
	- 13 * a1[12]
	- 17 * a1[16]
	- 18 * a1[17] == 7660269)
	s.add(20 * a1[19] * 19 * a1[18]
	+ 14 * a1[13]
	+ 13 * a1[12]
	+ 11 * a1[10] * 10 * a1[9]
	- 12 * a1[11]
	+ a1[0]
	+ 2 * a1[1]
	- (4 * a1[3] * 3 * a1[2]
	- 5 * a1[4]
	- 30 * a1[5])
	- 7 * a1[6]
	+ 8 * a1[7]
	- 9 * a1[8]
	- 16 * a1[15] * 15 * a1[14]
	- 17 * a1[16]
	- 18 * a1[17] == 2461883)
	s.add(
	14 * a1[13]
	+ 11 * a1[10] * 10 * a1[9]
	+ 9 * a1[8] * 8 * a1[7]
	+ 7 * a1[6]
	+ 2 * a1[1] * a1[0]
	- 4 * a1[3] * 3 * a1[2]
	- 5 * a1[4]
	- 30 * a1[5]
	- 12 * a1[11]
	- 13 * a1[12]
	- 15 * a1[14]
	- 17 * a1[16] * 16 * a1[15]
	- 18 * a1[17]
	- 19 * a1[18]
	- 20 * a1[19] == -966296)

	s.add(
	14 * a1[13]
	+ 13 * a1[12]
	+ (11 * a1[10] * 10 * a1[9] + 30 * a1[5] + 5 * a1[4] + 3 * a1[2] + 4 * a1[3] - 7 * a1[6] + 8 * a1[7] - 9 * a1[8])
	* 2
	* a1[1]
	+ a1[0]
	- 12 * a1[11]
	- 15 * a1[14]
	- 16 * a1[15]
	- 17 * a1[16]
	- 18 * a1[17]
	- 20 * a1[19] * 19 * a1[18] == 254500223
	)
	s.add(
	16 * a1[15] * 15 * a1[14]
	+ 14 * a1[13]
	+ 11 * a1[10] * 10 * a1[9]
	+ 7 * a1[6] * 30 * a1[5]
	+ a1[0]
	- 2 * a1[1]
	- 3 * a1[2]
	- 5 * a1[4] * 4 * a1[3]
	+ 8 * a1[7]
	- 9 * a1[8]
	- 12 * a1[11]
	- 13 * a1[12]
	- 17 * a1[16]
	- 18 * a1[17]
	- 19 * a1[18]
	- 20 * a1[19] == 6022286
	)
	s.add(
	18 * a1[17]
	+ 16 * a1[15]
	- 17 * a1[16]
	+ 14 * a1[13]
	+ 12 * a1[11]
	+ 11 * a1[10] * 10 * a1[9]
	+ 30 * a1[5]
	+ 5 * a1[4]
	+ 4 * a1[3] * 3 * a1[2]
	+ 2 * a1[1] * a1[0]
	- 9 * a1[8] * 8 * a1[7] * 7 * a1[6]
	- 13 * a1[12]
	- 15 * a1[14]
	- 19 * a1[18]
	- 20 * a1[19] == -636956022
	)
	s.add(
	20 * a1[19] * 19 * a1[18]
	+ 13 * a1[12]
	+ 12 * a1[11]
	+ 11 * a1[10] * 10 * a1[9]
	+ 7 * a1[6]
	+ 30 * a1[5]
	+ 5 * a1[4]
	+ 3 * a1[2] * 2 * a1[1] * a1[0]
	- 4 * a1[3]
	- 9 * a1[8] * 8 * a1[7]
	- 14 * a1[13]
	- 15 * a1[14]
	- 16 * a1[15]
	- 17 * a1[16]
	- 18 * a1[17] == 10631829
	)
	s.add(
	20 * a1[19] * 19 * a1[18]
	+ 16 * a1[15]
	- 17 * a1[16]
	- 18 * a1[17]
	+ 15 * a1[14] * 14 * a1[13]
	+ 13 * a1[12]
	+ 11 * a1[10] * 10 * a1[9]
	- 12 * a1[11]
	+ 7 * a1[6]
	+ (4 * a1[3] - 5 * a1[4] - 30 * a1[5]) * 3 * a1[2]
	+ a1[0]
	+ 2 * a1[1]
	+ 8 * a1[7]
	- 9 * a1[8] == 6191333
	)
	s.add(
	14 * a1[13]
	+ 10 * a1[9] * 9 * a1[8] * 8 * a1[7]
	+ 5 * a1[4]
	+ 4 * a1[3] * 3 * a1[2]
	+ 2 * a1[1] * a1[0]
	- 7 * a1[6] * 30 * a1[5]
	- 11 * a1[10]
	- 13 * a1[12] * 12 * a1[11]
	- 16 * a1[15] * 15 * a1[14]
	- 18 * a1[17] * 17 * a1[16]
	- 20 * a1[19] * 19 * a1[18] == 890415359
	)
	s.add(
	20 * a1[19]
	+ 19 * a1[18]
	+ 18 * a1[17]
	+ 16 * a1[15]
	- 17 * a1[16]
	+ 12 * a1[11]
	+ 11 * a1[10]
	+ 10 * a1[9]
	+ 9 * a1[8]
	+ 30 * a1[5]
	+ a1[0]
	+ 4 * a1[3] * 3 * a1[2] * 2 * a1[1]
	- 5 * a1[4]
	- 7 * a1[6]
	+ 8 * a1[7]
	- 13 * a1[12]
	- 14 * a1[13]
	- 15 * a1[14] == 23493664
	)
	s.add(
	20 * a1[19] * 19 * a1[18]
	+ 13 * a1[12]
	+ 12 * a1[11]
	+ 10 * a1[9]
	+ 3 * a1[2] * 2 * a1[1]
	+ a1[0]
	- 4 * a1[3]
	- 5 * a1[4]
	+ 8 * a1[7] * 7 * a1[6] * 30 * a1[5]
	- 9 * a1[8]
	- 11 * a1[10]
	- 14 * a1[13]
	- 16 * a1[15] * 15 * a1[14]
	- 17 * a1[16]
	- 18 * a1[17] == 1967260144
	)
	flag = []
	strflag = ''
	if s.check() == sat: # 检测是否有解
	result = s.model()
	for i in a1: # 因为最后得出的是等式，先遍历 a1，把 a1 的每个依次赋给 i
	flag.append(result[i]) # 然后找到每个 a1 对应的解，附加到空列表的后面
	print(flag)
	else:
	print('无解')
	#得 [104, 97, 104, 97, 104, 97, 116, 104, 105, 115, 105, 115, 102, 97, 99, 107, 102, 108, 97, 103]

注意 Z3 约束求解器 - 初始化序列时选择正确的格式比如这里就是 int 型序列

得第二次输入为 [104, 97, 104, 97, 104, 97, 116, 104, 105, 115, 105, 115, 102, 97, 99, 107, 102, 108, 97, 103]

z3 的数据在这里用到，又 weneed 比较数据已知可求出数组 tempp

	cp=[0x00001207, 0x00004CA0, 0x00004F21, 0x00000039, 0x0001A523, 0x0000023A, 0x00000926, 0x00004CA7, 0x00006560, 0x00000036, 0x0001A99B, 0x00004CA8, 0x0001BBE0, 0x00003705, 0x00000926, 0x000077D3, 0x00009A98, 0x0000657B, 0x00000018, 0x00000B11]
	z33=[104, 97, 104, 97, 104, 97, 116, 104, 105, 115, 105, 115, 102, 97, 99, 107, 102, 108, 97, 103]
	for i in range(len(cp)):
	cp[i]^=z33[len(cp)-i-1]
	print(cp)

cp (比较数据) 与倒过来的 z33 数据异或得 tempp 数组 [4704, 19649, 20301, 95, 107848, 601, 2375, 19649, 25875, 95, 109032, 19649, 113544, 14193, 2375, 30651, 39673, 25875, 121, 2937]

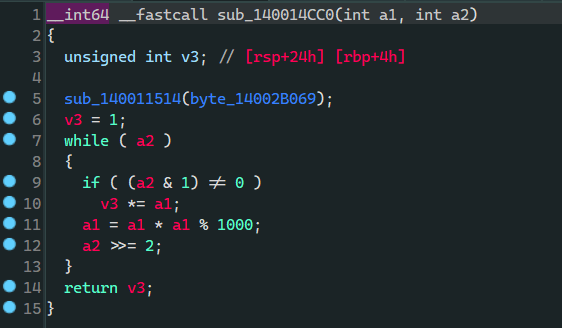
最后的关键在这一步函数，又因为函数的第二个参数是 int 数组 somenum 已知，tempp 已知，直接爆破 flag

C 语言爆破脚本如下

#include <stdio.h>
#include <string.h>
int baopo(int a1, int a2){
    {
  unsigned int v3; 
  v3 = 1;
  while ( a2 )
  {
    if ( (a2 & 1) != 0 )
      v3 *= a1;
    a1 = a1 * a1 % 1000;
    a2 >>= 2;
  }
  return v3;
}
}
int main(){
    unsigned int somenum[20] = {
    0x00000007, 0x00000007, 0x00000007, 0x00000009, 0x00000005, 0x00000006, 0x00000007, 0x00000007, 
    0x00000007, 0x00000009, 0x00000007, 0x00000007, 0x00000005, 0x00000007, 0x00000007, 0x00000007, 
    0x00000005, 0x00000007, 0x00000009, 0x00000007
};
int cp[20]={4704, 19649, 20301, 95, 107848, 601, 2375, 19649, 25875, 95, 109032, 19649, 113544, 14193, 2375, 30651, 39673, 25875, 121, 2937};
    int flag[20]={0};
    for(int i=0; i<20; i++){
        
        while (baopo(flag[i],somenum[i]) != cp[i])
        {
         flag[i]++;
        };
        printf("%d ",flag[i]);
    
}
}

运行结果 84 49 101 95 122 51 95 49 115 95 118 49 114 57 95 51 97 115 121 33

转字符即为 flag: T1e_z3_1s_v1r9_3asy! 把 flag 用给定的格式包起来提交就行了

# ctfshow 愚人杯 RE

除了一道抽象谜语题其他挺简单的我都能一眼丁真

# easy_pyc

先解 pyc 发现很简单不过就 114514 有点迷惑性其实可以直接去掉我直接 z3 解出

# 脚本及 flag

	from z3 import *
	code = [ 0x16, 0x1d, 0x1e, 0x1a, 0x18, 0x09, 0xff, 0xd0, 0x2c, 0x03, 0x02, 0x14, 0x38, 0x6d, 0x01, 0x43, 0x44, 0xbd, 0xf7,
	0x2a, 0x0d, 0xda, 0xf9, 0x1c, 0x26, 0x35, 0x27, 0xda, 0xd4, 0xd1, 0x0b, 0xc7, 0xc7, 0x1a, 0x90, 0x44, 0xa1]

	l = len(code)
	codec=[]
	a1 = [BitVec('x%d' % i, 32) for i in range(l)]
	s = Solver()
	for i in range(l):
	num = ((a1[i] + i) )
	codec.append(num)
	for i in range((l - 4) + 1):
	codec[i] = codec[i] ^ codec[i + 1]
	for i in range(l):
	s.add(codec[i]==code[i])
	flag = []
	if s.check() == sat: # 检测是否有解
	result = s.model()
	for i in a1: # 因为最后得出的是等式，先遍历 a1，把 a1 的每个依次赋给 i
	flag.append(result[i]) # 然后找到每个 a1 对应的解，附加到空列表的后面
	print(flag)
	else:
	print('无解')
	str=''
	flag=[99, 116, 102, 115, 104, 111, 119, 123, 74, 117, 115, 116, 95, 70, 48, 48, 108, 39, 115, 95, 68, 64, 121, 95, 82, 51, 95, 67, 104, 51, 99, 107, 45, 105, 110, 33, 125]
	for i in range(len(flag)):
	str+=chr(flag[i])
	print(str)

ctfshow

# easy_cc

32 位 IDA 打开程序逻辑很简单直接解上脚本

	eee=[0x08,0x11,0x1f,0x42,0x5a,0x5c,0x1c,0x1e,0x1a,0x52,0x6d,0x41,0x0e,0x3a,0x1e,0x5e,0x5d,0x57,0x34,0x02,0x16,0x5e,0x56,0x12,0x16]

	key='key123'
	key=list(key)
	v17=[]
	for i in range(len(eee)):
	v17.append((eee[i])^ord(key[i%len(key)]))
	print(v17)
	strr=''
	for i in range(len(v17)):
	strr+=chr(v17[i])
	print(strr)

ctfshow

# babyre

动调

提取的比较数据 [0x79, 0x8F, 0xAA, 0xEE, 0x69, 0x6A, 0x65, 0x53, 0x2B, 0xEE, 0x7B, 0x80, 0x9B, 0xD7, 0x7D, 0x9B, 0xD0, 0x2B, 0xE8, 0x71, 0x7E, 0x9B, 0xBD, 0xFD]

看看加密函数

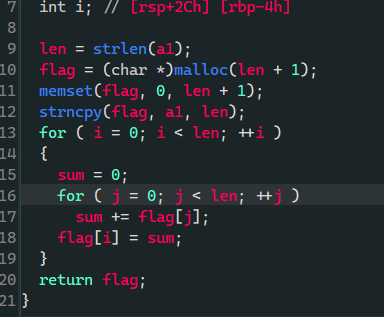
我直接开爆 (其实是 z3)

	from z3 import *
	temp = [BitVec('x%d' % i, 8) for i in range(24)] # 初始化序列
	s = Solver() # 创建约束求解器

	cp=[0x79, 0x8F, 0xAA, 0xEE, 0x69, 0x6A, 0x65, 0x53, 0x2B, 0xEE, 0x7B, 0x80, 0x9B, 0xD7, 0x7D, 0x9B, 0xD0, 0x2B, 0xE8, 0x71, 0x7E, 0x9B, 0xBD, 0xFD]
	l=len(cp)
	sum=0
	for i in range(l):
	sum=0
	for j in range(l):
	sum=temp[j]+sum
	temp[i]=sum
	for i in range(l):
	s.add(cp[i]==temp[i])
	print(s.check())
	flag=[]
	result = s.model()
	print(result)

	-----------------get flag-------------------
	flag=[99,116,102,115,104,111,119,123,104,97,118,101, 95,49,95,102,117,110,95,100,97,121,125]
	strr=''
	for i in range(len(flag)):
	strr+=chr(flag[i])
	print(strr)
	#ctfshow{have_1_fun_day}

弗拉格为 ctfshow

# easy_re

32 位直接 IDA

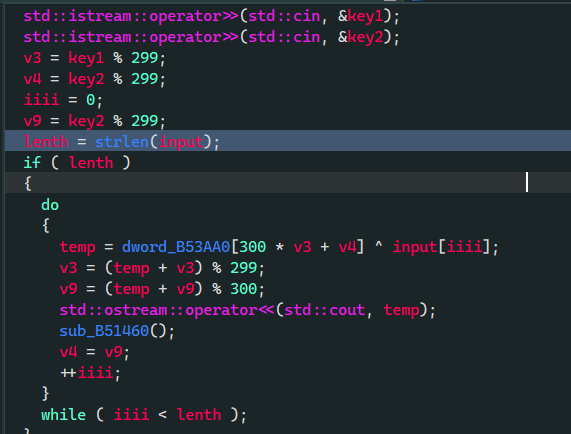
逻辑也很清晰问题是获取 key 可以通过爆破？后面怎么办做不来摆烂了等 wp

# not_a_like

NKCTF 一道题，和前面的 ez_z3 类似魔改的 UPX 壳，不同的是它不是修改了区段头名字而是直接抹去了

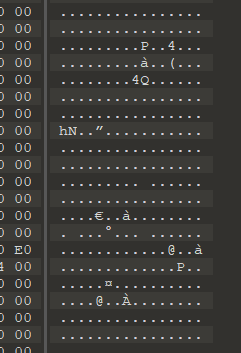
和正常的一对比就能补充上头部了

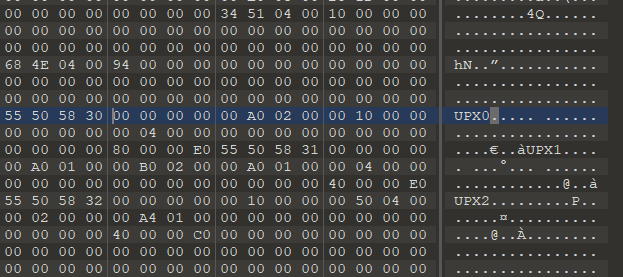
(其实位置没有规定的那么固定)

直接解 upx 然后放进 IDA 中看可判断为 py 打包 (也可从程序的大小很大看出)

直接 python pyinstxtractor.py not_a_like.exe (这里其实警告说是 python3.8 我是 3.10 但发现没影响后面)

直接找在线工具解密 pyc 得以下 py 脚本

	#!/usr/bin/env python
	# visit https://tool.lu/pyc/ for more information
	# Version: Python 3.8

	import libnum
	import base64
	import hashlib
	from ctypes import *

	def encrypt(text):
	data_xor_iv = bytearray()
	sbox = []
	j = 0
	x = y = k = 0
	key = '911dcd09ad021d68780e3efed1aa8549'
	for i in range(256):
	sbox.append(i)
	for i in range(256):
	j = j + sbox[i] + ord(key[i % len(key)]) & 255
	sbox[i] = sbox[j]
	sbox[j] = sbox[i]
	for idx in text:
	x = x + 1 & 255
	y = y + sbox[x] & 255
	sbox[x] = sbox[y]
	sbox[y] = sbox[x]
	k = sbox[sbox[x] + sbox[y] & 255]
	data_xor_iv.append(idx ^ k)
	return data_xor_iv

	if __name__ == '__main__':
	flag = input('%e8%af%b7%e8%be%93%e5%85%a5flag> ')
	pub_key = [
	0x1B6A7561D99E6FC35BA3C241159424698BF3CAC017CFCE8BB325CC9AF9CBCBDB3997B08D922C8705FC3EEAEF50D60ADAB2757A7204715483A1D612502970595358BCFE9CD11C98CAD293EB921D777F4F910905D79CDCA5C1EC1FBA5DA74DB165F82BBE29EA0B2E597860FC6D2C51C12D46BF11AFA5018496DDFC3474B10B4457L,
	0x6C8E1CC5B384DE3B3316C22CF72D9895406298E172B5F4D890BDC04889BB43CD4892689DE701C84ED68B4CBC7193926BCCB0A4F259D2E752FAEF3CD590A793F120D15424AEB3CD53F5D59B5D41D699694ABF4F01532F0F1CE127B07958FB874982E757EF97643335376790BC990CEE9D7F0D05DA90AD62084C88BFA9C9BEB683L]
	m = libnum.s2n(flag)
	c = str(pow(m, pub_key[0], pub_key[1]))
	q = b'EeJWrgtF+5ue9MRiq7drUAFPtrLATlBZMBW2CdWHRN73Hek7DPVIYDHtMIAfTcYiEV87W7poChqpyUXYI3+/zf5yyDOyE9ARLfa5qilXggu60lmQzFqvFv+1uOaeI2hs2wx+QZtxqGZzC0VCVWvbTQ52nA2UdUtnk8VezRMPMfmf7rOqPxDTv/aacLnI3RdLG2TbT52qtN4+naejI7Xe8HLOL765OZKdDBERKwd5ARQ3UL6YPbuOKOQahIFddnIX6rZ7dTNqCUDOjfJbMdrzJVDNjmNlkLNtYFo7M65Wfwj6PV5vvtT33FsmH50/YLEasnlCiJujYOgi2KCdf5msz1dPEvrXDDL6Csnjo+6m/44RzlluzcqMS5ZJFdrHEh68LIqtu+HCO+69Dyq4e22APq8wgN9kU6R8kikXSn/Ej0N/jOvomFCbkHskRl8xP1KgWFW0SMVDlaDCM4EKG812VgDWgSYOUnVhVpz65uOtg4Z8PrPI+BW4398dQYhD24D9EIPgvtmhNrHiEHouB46ElTGQgZBhtn6y9tL1sw=='
	v = encrypt(base64.b64encode(c.encode('utf-8')))
	v = base64.b64encode(v)
	if v == q:
	print('You are right!')
	input('')
	else:
	print('winer winer winnie dinner')
	print('Do you think the encryption and decryption are the same?')

分析逻辑知输入 flag 后先是 RSA 加密，再 base64 加密，再 RC4 加密，再 base64 加密又比较数据已知直接找脚本或工具解就行了

附上一个包括了所有解密的完整脚本

	import base64, gmpy2, libnum


	def continuedFra(x, y):
	cf = []
	while y:
	cf.append(x // y)
	x, y = y, x % y
	return cf


	def gradualFra(cf):
	numerator = 0
	denominator = 1
	for x in cf[::-1]:
	numerator, denominator = denominator, x * denominator + numerator
	return numerator, denominator


	def solve_pq(a, b, c):
	par = gmpy2.isqrt(b * b - 4 * a * c)
	return (-b + par) // (2 * a), (-b - par) // (2 * a)


	def getGradualFra(cf):
	gf = []
	for i in range(1, len(cf) + 1):
	gf.append(gradualFra(cf[:i]))
	return gf


	def wienerAttack(e, n):
	cf = continuedFra(e, n)
	gf = getGradualFra(cf)
	for d, k in gf:
	if k == 0: continue
	if (e * d - 1) % k != 0:
	continue
	phi = (e * d - 1) // k
	p, q = solve_pq(1, n - phi + 1, n)
	if p * q == n:
	return d


	c = bytearray()
	pub_key = [
	19252067118061066631831653736874168743759225404757996498452383337816071866700225650384181012362739758314516273574942119597579042209488383895276825193118297972030907899188520426741919737573230050112614350868516818112742663713344658825493377512886311960823584992531185444207705213109184076273376878524090762327,
	76230002233243117494160925838103007078059987783012242668154928419914737829063294895922280964326704163760912076151634681903538211391318232043295054505369037037489356790665952040424073700340441976087746298068796807069622346676856605244662923296325332812844754859450419515772460413762564695491785275009170060931]
	q = b'EeJWrgtF+5ue9MRiq7drUAFPtrLATlBZMBW2CdWHRN73Hek7DPVIYDHtMIAfTcYiEV87W7poChqpyUXYI3+/zf5yyDOyE9ARLfa5qilXggu60lmQzFqvFv+1uOaeI2hs2wx+QZtxqGZzC0VCVWvbTQ52nA2UdUtnk8VezRMPMfmf7rOqPxDTv/aacLnI3RdLG2TbT52qtN4+naejI7Xe8HLOL765OZKdDBERKwd5ARQ3UL6YPbuOKOQahIFddnIX6rZ7dTNqCUDOjfJbMdrzJVDNjmNlkLNtYFo7M65Wfwj6PV5vvtT33FsmH50/YLEasnlCiJujYOgi2KCdf5msz1dPEvrXDDL6Csnjo+6m/44RzlluzcqMS5ZJFdrHEh68LIqtu+HCO+69Dyq4e22APq8wgN9kU6R8kikXSn/Ej0N/jOvomFCbkHskRl8xP1KgWFW0SMVDlaDCM4EKG812VgDWgSYOUnVhVpz65uOtg4Z8PrPI+BW4398dQYhD24D9EIPgvtmhNrHiEHouB46ElTGQgZBhtn6y9tL1sw=='
	e = pub_key[0]
	n = pub_key[1]

	# 恢复 c
	v = base64.b64decode(q)
	data_xor_iv = bytearray()
	sbox = []
	j = 0
	x = y = k = 0
	key = '911dcd09ad021d68780e3efed1aa8549'
	for i in range(256):
	sbox.append(i)

	for i in range(256):
	j = j + sbox[i] + ord(key[(i % len(key))]) & 255
	sbox[i], sbox[j] = sbox[j], sbox[i]

	for idx in v:
	x = x + 1 & 255
	y = y + sbox[x] & 255
	sbox[x], sbox[y] = sbox[y], sbox[x]
	k = sbox[(sbox[x] + sbox[y] & 255)]
	c.append(idx ^ k)
	c = int(base64.b64decode(bytes(c)))


	# 维纳攻击
	d = wienerAttack(e, n)
	m = pow(c, d, n)
	print(libnum.n2s(m).decode())

笔记